

Whispering-gallery wave. Whispering-gallery waves, or whispering-gallery modes, are a type of wave that can travel around a concave surface.
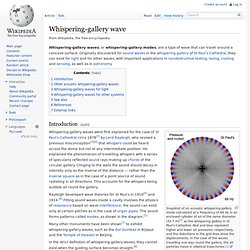
Originally discovered for sound waves in the whispering gallery of St Paul’s Cathedral, they can exist for light and for other waves, with important applications in nondestructive testing, lasing, cooling and sensing, as well as in astronomy. Ellipse. Was ist eine Ellipse?

Mittelpunktsgleichung topMit diesem Ansatz gelangt man zu der "Mittelpunktsgleichung" der Ellipse: x²/a²+y²/b²=1.Die Variablen a und b stehen für positive reelle Zahlen. Herleitung der MittelpunktsgleichungDurch zweimaliges Quadrieren werden die Wurzelterme entfernt. Die Gleichung heißt dann a²x²-e²x²+a²y²+a²e²-(a²)²=0 <=> (a²-e²)x²+a²y²=a²(a²-e²) Führt man die Variable b über b²=a²-e² ein, so vereinfacht sich die Gleichung zu b²x²+a²y²=a²b² oder x²/a²+y²/b²=1, wzbw.. Zahlenbeispiel Diskussion der Ellipsengleichung topDefinitionsbereichDie Gleichung x²/a²+y²/b²=1 ergibt, nach y aufgelöst, y=+(b/a)sqrt(a²-x²) und y=-(b/a)sqrt(a²-x²). Deutung von a und bZur Entfernung der Brennpunkte 2e SymmetrieDa die Gleichung x²/a²+y²/b²=1 sich nicht ändert, wenn man x durch -x und/oder y durch -y ersetzt, ist die Ellipse symmetrisch bezüglich der Achsen.
Ellipsenscharen topAlle Formen der EllipseIst a=b, so artet die Ellipse zu einem Kreis aus. Spherical polyhedron. This beach ball shows a hosohedron with six lune faces, if the white circles on the ends are removed.
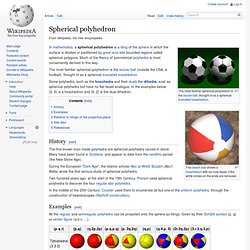
In mathematics, a spherical polyhedron is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra is most conveniently derived in this way. The most familiar spherical polyhedron is the soccer ball (outside the USA, a football), thought of as a spherical truncated icosahedron. Some polyhedra, such as the hosohedra and their duals the dihedra, exist as spherical polyhedra but have no flat-faced analogue. List of circle topics. List of circle topics From Wikipedia, the free encyclopedia Jump to: navigation, search This list of circle topics includes things related to the geometric shape, either abstractly, as in idealizations studied by geometers, or concretely in physical space.
It does not include metaphors like "inner circle" or "circular reasoning" in which the word does not refer literally to the geometric shape. Contents. Circle. A circle can be defined as the curve traced out by a point that moves so that its distance from a given point is constant.
Terminology[edit] Cartesian oval. Example of Cartesian ovals.
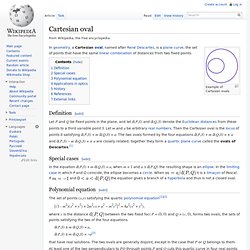
In geometry, a Cartesian oval, named after René Descartes, is a plane curve, the set of points that have the same linear combination of distances from two fixed points. Definition[edit] Special cases[edit] Cassini oval. Some Cassini ovals.
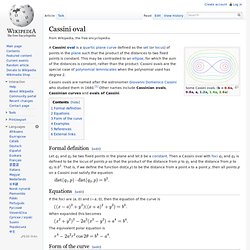
(b = 0.6a, 0.8a, a, 1.2a, 1.4a, 1.6a) Cassini ovals are named after the astronomer Giovanni Domenico Cassini who studied them in 1680.[1] Other names include Cassinian ovals, Cassinian curves and ovals of Cassini. Formal definition[edit] Laplace–Runge–Lenz vector. The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse square central force.
The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom,[3] before the development of the Schrödinger equation. However, this approach is rarely used today. In classical and quantum mechanics, conserved quantities generally correspond to a symmetry of the system. The Laplace–Runge–Lenz vector is named after Pierre-Simon de Laplace, Carl Runge and Wilhelm Lenz. Eccentricity vector. Calculation[edit] The eccentricity vector can be calculated[1] where: or equivalently: See also[edit] References[edit]
Orbital eccentricity. An elliptic Kepler orbit with an eccentricity of 0.7 (red ellipse), a parabolic Kepler orbit (green) and a hyperbolic Kepler orbit with an eccentricity of 1.3 (blue outer line) The orbital eccentricity of an astronomical object is a parameter that determines the amount by which its orbit around another body deviates from a perfect circle.
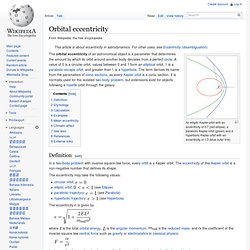
A value of 0 is a circular orbit, values between 0 and 1 form an elliptical orbit, 1 is a parabolic escape orbit, and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the galaxy. Eccentricity (mathematics) All types of conic sections, arranged with increasing eccentricity. Note that curvature decreases with eccentricity, and that none of these curves intersect. Ellipsoid method. An iteration of the ellipsoid method In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions.
When specialized to solving feasible linear optimization problems with rational data, the ellipsoid method is an algorithm which finds an optimal solution in a finite number of steps. The ellipsoid method generates a sequence of ellipsoids whose volume uniformly decreases at every step, thus enclosing a minimizer of a convex function. History[edit] The ellipsoid method has a long history. Following Khachiyan's work, the ellipsoid method was the only algorithm for solving linear programs whose runtime had been proved to be polynomial until Karmarkar's algorithm. Description[edit] Ellipsoid. Tri-axial ellipsoid with distinct semi-axis lengths. Ellipse. The rings of Saturn are circular, but when seen partially edge on, as in this image, they appear to be noncircular ellipses. In addition, the planet itself is an ellipsoid, flatter at the poles than the equator. Picture by ESO Ellipses are common in physics, astronomy and engineering. Great-circle distance.
Through any two points on a sphere which are not directly opposite each other, there is a unique great circle. Spherical trigonometry. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam. The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's text book Spherical trigonometry for the use of colleges and Schools. This book is now readily available on the web.[1] The only significant developments since then have been the application of vector methods for the derivation of the theorems and the use of computers to carry through lengthy calculations. Preliminaries[edit] Eight spherical triangles defined by the intersection of three great circles.