

Algebra/Trig Review - Solving Trig Equations. Solve the following trig equations.
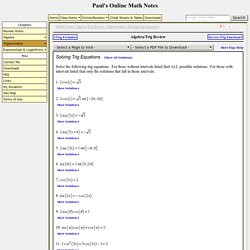
For those without intervals listed find ALL possible solutions. For those with intervals listed find only the solutions that fall in those intervals. There’s not much to do with this one. Just divide both sides by 2 and then go to the unit circle. So, we are looking for all the values of t for which cosine will have the value of . From quick inspection we can see that is a solution. . To find this angle for this problem all we need to do is use a little geometry. With the positive x-axis, then so must the angle in the fourth quadrant. . , but again, it’s more common to use positive angles so, we’ll use We aren’t done with this problem. That we want for the solution and sometimes we will want both (or neither) of the listed angles. This is very easy to do. Mc-ty-trigeqn-2009-1.pdf.
Lesson HOW TO - Solve Trigonometric equations. Introduction The solution of trigonometric equations is one topic that students have particular problems with.
There are a few reasons for this: 1. there is usually a simplify part first that requires use of some TRIG identities. 2. there is the use of RADIANS rather than degrees, for which some students are not at ease with. 3. there is the repetitive aspect of TRIG functions that students find bewildering. All in all, a potentially daunting topic. To be honest though, there is nothing that you need fear here, so long as you take it methodically and slowly. Also, you have to understand what it is you are doing. Solving the TRIG Equation Of the 3 topics listed above, I am concentrating on part 3, here in this Lesson. First thing, when solving a TRIG equation, is to understand or accept that each of SINE, COSINE and TANGENT have 2 angles that will satisfy the given equation within any 360 degree range. Basics This is difficult to explain, with no real picture to use, so bear with me.
Done! Trig_From_Quadrant_I_to_All_Four.pdf. Graphing%20Trig%20Functions.pdf. Graphing Trigonometric Functions. Graphing Trigonometric Functions (page 1 of 3) Sections: Introduction, Examples with amplitude and vertical shift, Example with phase shift You've already learned the basic trig graphs.
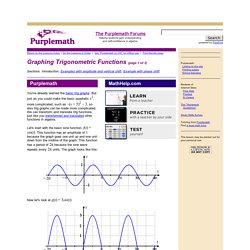
But just as you could make the basic quadratic x2, more complicated, such as –(x + 5)2 – 3, so also trig graphs can be made more complicated. We can transform and translate trig functions, just like you transformed and translated other functions in algebra. Let's start with the basic sine function, f(t) = sin(t). Now let's look at g(t) = 3sin(t): Do you see that the graph is three times as tall? Now let's look at h(t) = sin(2t): Copyright © Elizabeth Stapel 2010 All Rights Reserved Do you see that the graph is squished in from the sides? For sines and cosines (and their reciprocals), the "regular" period is 2π, so the formula is: For tangents and cotangents, the "regular" period is π, so the formula is: In the sine wave graphed above, the value of B was 2.
Now let's looks at j(t) = sin(t – π/3): SOLVING TRIGONOMETRIC EQUATIONS. Note: If you would like a review of trigonometry, click on trigonometry.

Example 1: Solve for x in the following equation. There are an infinite number of solutions to this problem. First isolate the cosine term. To solve for x, we have to isolate x. How do we isolate the x? Let's restrict the domain so the function is one-to-one on the restricted domain while preserving the original range. If we restrict the domain of the cosine function to that interval , we can take the arccosine of both sides of each equation. The angle x is the reference angle. Therefore, if , then.