

Beta. In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] parametrized by two positive shape parameters, denoted by α and β, that appear as exponents of the random variable and control the shape of the distribution.
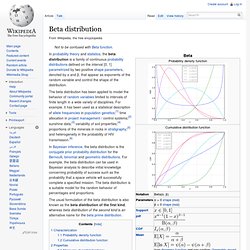
The beta distribution has been applied to model the behavior of random variables limited to intervals of finite length in a wide variety of disciplines. For example, it has been used as a statistical description of allele frequencies in population genetics;[1] time allocation in project management / control systems;[2] sunshine data;[3] variability of soil properties;[4] proportions of the minerals in rocks in stratigraphy;[5] and heterogeneity in the probability of HIV transmission.[6] In Bayesian inference, the beta distribution is the conjugate prior probability distribution for the Bernoulli, binomial and geometric distributions.
Characterization[edit] Arcsine. In probability theory, the arcsine distribution is the probability distribution whose cumulative distribution function is for 0 ≤ x ≤ 1, and whose probability density function is on (0, 1).
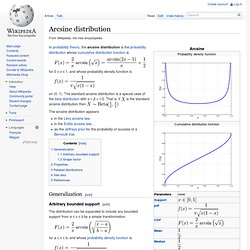
The standard arcsine distribution is a special case of the beta distribution with α = β = 1/2. That is, if. Uniform. The probability density function of the continuous uniform distribution is: The values of f(x) at the two boundaries a and b are usually unimportant because they do not alter the values of the integrals of f(x) dx over any interval, nor of x f(x) dx or any higher moment.
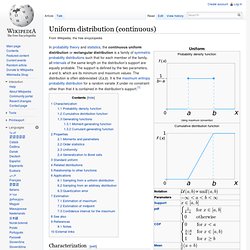
Sometimes they are chosen to be zero, and sometimes chosen to be 1/(b − a). The latter is appropriate in the context of estimation by the method of maximum likelihood. In the context of Fourier analysis, one may take the value of f(a) or f(b) to be 1/(2(b − a)), since then the inverse transform of many integral transforms of this uniform function will yield back the function itself, rather than a function which is equal "almost everywhere", i.e. except on a set of points with zero measure. Also, it is consistent with the sign function which has no such ambiguity.