

¿Quién inventó los números? - CuriosaMente 123. Intervalos: Definición y ejemplos. ¿Qué es Pi? - CuriosaMente T3E02. (Los Números) - Sistemas de Numeración (401) La Eduteca - Los números romanos. Númeración Romana. 1. Números naturales. Sistema de Numeración decimal. Sistema sexagesimal. Upload unProfesor.com unProfesor Loading...
Working... ► Play all Sistema sexagesimal unProfesor10 videos1,257 viewsLast updated on Dec 9, 2015 Play all Sign in to YouTube Sign in History Sign in to add this to Watch Later Add to. (Los Números) - Sistema Binario (402) El código binario. Convertir un número decimal a binario. (Los Números) - Conjuntos Numéricos (404) Clasificación de los números reales. Troncho y Poncho Numéros Naturales y Enteros. Los Números Reales: propiedades y operaciones básicas. Upload www.academiajaf.com academia JAF Loading...
Working... ► Play all Los Números Reales: propiedades y operaciones básicas academia JAF16 videos7,099 viewsLast updated on Aug 9, 2015 Play all Sign in to YouTube Sign in History Sign in to add this to Watch Later. Números reales. Upload unProfesor.com.
Los números complejos. Upload unProfesor.com unProfesor Loading...
Working... Los Pitagóricos y los Irracionales. Pi es 3 exactamente! ¿Qué es el número e? El número de Oro (1,61803398874988...) Nature by Numbers. Números Reales para 4º ESO (Genmagic) - Didactalia: material educativo. Grandes temas de la matemática: Capítulo 1: El número PI. Grandes temas de la matemática: Capítulo 5: Número E. Demostración de que raíz de 2 es irracional. Intervalos. Tipos. Representación. Intersección de intervalos. Unión de intervalos. Intervalo cerrado y abierto. Intervalos: Definición y ejemplos. Intervalos Unión e Intersección. Representar gráficamente intervalos - HD. Intervalos, definición y uso. Aprende matemáticas. Operaciones con intervalos: reunión, intersección, diferencia y complemento. Sin Números. ¿Es fácil encontrar números amigos?
El Hotel Infinito. Grandes temas de la matemática: Capítulo 13: Infinito. La sucesión de Fibonacci y la razón aúrea. Grandes temas de la matemática: Capítulo 4: Fibonacci. Teorías fantásticas sobre el origen de la grafía de las cifras. Recientemente alguien me ha recordado en twitter un “famoso” powerpoint que circuló hace algunos años por la red, y que fue enviado masivamente a través del correo electrónico (a mí me llegó varias veces).
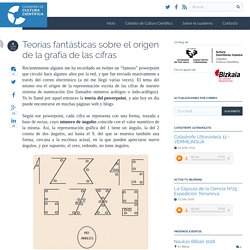
El tema del mismo era el origen de la representación escrita de las cifras de nuestro sistema de numeración (los llamados números arábigos o indo-arábigos). Yo lo llamé por aquel entonces la teoría del powerpoint, y aún hoy en día puede encontrarse en muchas páginas web y blogs. Según ese powerpoint, cada cifra se representa con una forma, trazada a base de rectas, cuyo número de ángulos coincide con el valor numérico de la misma.
Así, la representación gráfica del 1 tiene un ángulo, la del 2 consta de dos ángulos, así hasta el 9, del que se muestra también una forma, cercana a la escritura actual, en la que pueden apreciarse nueve ángulos, y por supuesto, el cero, redondo, no tiene ángulos. Seguro que vosotros también lo recibisteis en alguna ocasión. Según Howard W. ¿Por qué un folio es de tamaño DIN A4? Estenmáticas. 2º ESO. Ejercicio 6. Aplicaciones de Pitágoras: raíces cuadradas. ¿Aún no tienes un número favorito? ¿Cuál es el número más grande? - CuriosaMente Ep3. Juan Manuel Sabugo - El n�mero cero: uno de los inventos m�s importantes de la historia. "Todo lo que hay, ha existido siempre.
Nada puede surgir de la nada. Y algo que existe, tampoco se puede convertir en nada". Parménides "¿Por qué hay algo en lugar de nada? ". Leibniz La nada es un concepto escurridizo. Los números: sus nombres y sus escrituras La India estaba muy adelantada en el campo de las matemáticas respecto al resto de los países gracias a su forma, muy particular, de escribir los números. La gran revolución impuesta por la India fue dotar al sistema de: por un lado, una numeración decimal en la que la colocación relativa de los números otorgaba un valor diferente a las cantidades; y por otro, la incorporación del "cero" para rellenar esas posiciones donde no había cantidades que contar.
La primera constancia de la utilización de este método se conserva en los grabados de una pared del Templo Chaturbhuj, un fuerte construido hace 1.200 años. Brahmagupta, el primer matemático. El origen del "cero" como concepto.