Structured diff
Get flash to fully experience Pearltrees
Longest common subsequence problem
The longest common subsequence ( LCS ) problem is to find the longest subsequence common to all sequences in a set of sequences (often just two). Note that subsequence is different from a substring, see substring vs. subsequence . It is a classic computer science problem, the basis of file comparison programs such as diff , and has applications in bioinformatics . [ edit ] Complexity For the general case of an arbitrary number of input sequences, the problem is NP-hard . [ 1 ] When the number of sequences is constant, the problem is solvable in polynomial time by dynamic programming (see Solution below). Assume you haveIn computer science , Hirschberg's algorithm , named after its inventor, Dan Hirschberg , is a dynamic programming algorithm that finds the optimal sequence alignment between two strings . Optimality is measured with the Levenshtein distance , defined to be the sum of the costs of insertions, replacements, deletions, and null actions needed to change one string into the other. Hirschberg's algorithm is simply described as a divide and conquer version of the Needleman–Wunsch algorithm . [ 1 ] Hirschberg's algorithm is commonly used in computational biology to find maximal global alignments of DNA and protein sequences.
Hirschberg's algorithm
In information theory and computer science , the Damerau–Levenshtein distance (named after Frederick J. Damerau and Vladimir I. Levenshtein ) is a "distance" ( string metric ) between two strings , i.e., finite sequence of symbols, given by counting the minimum number of operations needed to transform one string into the other, where an operation is defined as an insertion, deletion, or substitution of a single character, or a transposition of two adjacent characters. In his seminal paper [1] , Damerau not only distinguished these four edit operations but also stated that they correspond to more than 80% of all human misspellings. Damerau's paper considered only misspellings that could be corrected with at most one edit operation.
Damerau–Levenshtein distance
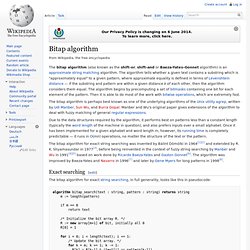
The bitap algorithm (also known as the shift-or , shift-and or Baeza–Yates–Gonnet algorithm) is an approximate string matching algorithm. The algorithm tells whether a given text contains a substring which is "approximately equal" to a given pattern, where approximate equality is defined in terms of Levenshtein distance — if the substring and pattern are within a given distance k of each other, then the algorithm considers them equal. The algorithm begins by precomputing a set of bitmasks containing one bit for each element of the pattern. Then it is able to do most of the work with bitwise operations , which are extremely fast. The bitap algorithm is perhaps best known as one of the underlying algorithms of the Unix utility agrep , written by Udi Manber , Sun Wu , and Burra Gopal . Manber and Wu's original paper gives extensions of the algorithm to deal with fuzzy matching of general regular expressions .
Bitap algorithm
Needleman–Wunsch algorithm
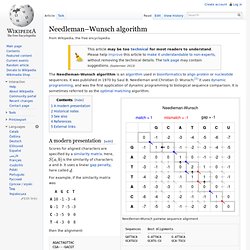
The Needleman–Wunsch algorithm performs a global alignment on two sequences (called A and B here). It is commonly used in bioinformatics to align protein or nucleotide sequences. The algorithm was published in 1970 by Saul B. Needleman and Christian D.
Smith–Waterman algorithm
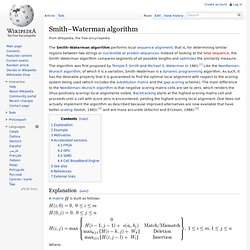
The Smith–Waterman algorithm performs local sequence alignment ; that is, for determining similar regions between two strings or nucleotide or protein sequences . Instead of looking at the total sequence , the Smith–Waterman algorithm compares segments of all possible lengths and optimizes the similarity measure . [ edit ] Background The algorithm was first proposed by Temple F. Smith and Michael S. Waterman in 1981. [ 1 ] Like the Needleman–Wunsch algorithm , of which it is a variation, Smith–Waterman is a dynamic programming algorithm.
Matching, diffing and merging XML
Update : A newer, more complete version is here . I've said bad things about my job working on Carleton College's website, but fundamentally it's a really sound work environment we have. Just before winter break, one of the full-time employees came to me and asked if I could make a diff between two XHTML documents for use in Carleton's CMS, Reason. This would be useful for (a) comparing versions of a document in the CMS (b) merging documents, in case two people edit the same document at the same time, so as to avoid locks and the need for manual merges. They came to me because I told them I'd written an XML parser.Daisy Diff is a Java library that diffs (compares) HTML files. It highlights added and removed words and annotates changes to the styling. ( Examples ) This project was a Google Summer of Code 2007 project for DaisyCMS where it's actively used for diffing HTML content. As a spin-off, a PHP version of the algorithm was developed for MediaWiki in the GSoC 2008 . The Java version is licensed under the Apache License v2. The PHP version is GPLv2+.
daisydiff - Project Hosting on Google Code
Java Notes
by Stuart D. Gathman Last updated Dec 08, 2010 I have moved the most popular items to the top of the menu. Class Packager for Java If you want to deliver an application or applet with all the classes and resources it needs - and only the classes and resources it needs, then you need ZipLock.java .
i’ve spent the last week trying to get my brain wrapped around the issues involved with performing XML comparisons and how they might be solved. i also decided early on in my reading and discussions that i’d better attack this problem in stages, otherwise i’d have nothing to show for it for a very long time. in other words, this is a non-trivial problem. at least for me <g> so what makes this a hard problem? after all, there’s a ton of “difference” programs out there, like diff, windiff, tkdiff, etc. why not take the two XML-documents to be compared and run one of these programs over them and see what it says? it will certainly tell us something, why can’t we stop there?