

Algorithme de Kruskal. Un article de Wikipédia, l'encyclopédie libre.
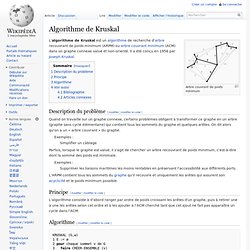
Arbre couvrant de poids minimum Description du problème[modifier | modifier le code] Quand on travaille sur un graphe connexe, certains problèmes obligent à transformer ce graphe en un arbre (graphe sans cycle élémentaire) qui contient tous les sommets du graphe et quelques arêtes. On dit alors qu'on a un « arbre couvrant » du graphe. Exemples : Simplifier un câblage Parfois, lorsque le graphe est valué, il s'agit de chercher un arbre recouvrant de poids minimum, c'est-à-dire dont la somme des poids est minimale.
Supprimer les liaisons maritimes les moins rentables en préservant l'accessibilité aux différents ports. L'ARPM contient tous les sommets du graphe qu'il recouvre et uniquement les arêtes qui assurent son acyclicité et le poids minimum possible. Principe[modifier | modifier le code] Algorithme[modifier | modifier le code] w est une fonction qui associe à chaque arête du graphe G une valeur qui est son poids. Thomas H. Algorithme de Prim. Un article de Wikipédia, l'encyclopédie libre.
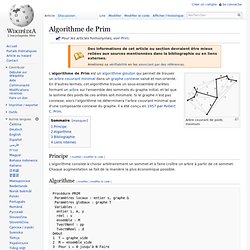
Pour les articles homonymes, voir Prim. Arbre couvrant de poids minimum Principe[modifier | modifier le code] L'algorithme consiste à choisir arbitrairement un sommet et à faire croître un arbre à partir de ce sommet. Chaque augmentation se fait de la manière la plus économique possible. Algorithme[modifier | modifier le code] Procédure PRIM Paramètres locaux : entier s, graphe G Paramètres globaux : graphe T Variables : entier i, m, y réel : v ensemble : M TvectNent : pp TvectNReel : d Début 1 T ← graphe_vide 2 M ← ensemble_vide 3 Pour i ← 0 jusqu'à N Faire 4 d[i] ←coût(s, i, G) 5 pp[i] ← s 6 M ← Ajouter (i,M) 7 Fin pour 8 M ← Supprimer (s,M) 9 Tant que M <> Ensemble_vide Faire 10 m ← Choisir (M,d) 11 M ← Supprimer (m,M) 12 z ← pp[m] 13 T ← Ajout arête <m,z> de coût d[m] à T 14 Pour i ← 1 jusqu'à d° m dans G Faire 15 y ← i ième_succ_de m dans G 16 Si y (Attention, le principe suivant diffère de l'implémentation proposée).
J. Peli\'s Farm - Fun with Graphs (4): Computing PageRank of a grap. As most of you should know by now, PageRank is the ranking system used by Google to estimate the importance of a page (you can see it in the Google toolbar).

Of course, since the basic idea of the algorithm was published they may have been some significant modifications. In this blog, I'll how we can use QuickGraph to compute the PageRank of a graph... PageRank The idea behind PageRank is simple and intuitive: pages that are important are referenced by other important pages, page importance is distributed to out-edges. There is an important literature on the web that explains PageRank: PR(A) = (1-d) + d (PR(T1)/C(T1) + ... + PR(Tn)/C(Tn)) where is the PageRank, is a damping factor usually set to 0.85, is the number of out edges of . PageRank can also be expressed in terms of matrix algebra where it is shown that it is equivalent to finding the eigen values of a sparse matrix (see And in fact, the above formula is equivalent to the Power Method (a slow method for finding eigen values).