

CvLAC. Logica. Página de ALEJANDRA RUBIO VANEGAS. Club Networking TIC. La importancia de las herramientas web 2.0 en la educación” Twitter. Test Autoevaluaci n de Conjuntos. conjuntos. Alejandra Rubio -... OVA LOGICA MATEMATICA. Proposiciones. AudioKiosko, podcast, radio, mp3 y más - iVoox. EJERCICIOS DE PROPOSICIONES_u. Humana.pdf. PowToon - Teacher Intro. Modelo APA Bibliografia. Tutorial: Como crear un mapa conceptual en Cmap Tools. LOGICA MATEMÁTICA by on Prezi. Perfil de ALEJANDRA RUBIO VANEGAS. Lógica, matemáticas y conceptualismo. EJERCICIOS. Hola mi nombre es Alex, y en ésta entrada del blog encontrarás problemas resueltos y propuestos de , la mayoría de los problemas los he resuelto en vídeo teniendo en mente que no sabes mucho de matematica, así que las explicaciones esta bien detalladas.
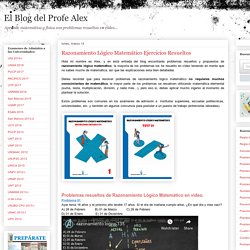
Debes recordar que para resolver problemas de razonamiento lógico matemático no requieres muchos conocimientos de matemática, la mayor parte de los problemas se resuelven utilizando matemática elemental (suma, resta, multiplicación, división, y nada más...), pero eso si, debes aplicar mucho ingenio al momento de plantear la solución. Estos problemas son comunes en los exámenes de admisión a institutos superiores, escuelas politécnicas, universidades, etc. y también en algunos concursos para postular a un puesto de trabajo (entrevistas laborales).
Ayer tenía 16 años y el próximo año tendré 17 años. Si el día de mañana cumplo años. ¿En qué día y mes nací? Ejercicio 1 Ejercicio 4 Se tiene tres ciudades M, N y P. Ejercicio 7 Ejercicio 25. Modus Ponendo Ponens. VALIDEZ DE UN RAZONAMIENTO DEDUCTIVO. Construcción Tablas de verdad. Razonamiento inductivo y deductivo. La psicología cognitiva ha basado fundamentalmente sus investigaciones en tres aspectos:- El razonamiento deductivo,- El razonamiento inductivo y- La resolución de problemas.
El pensamiento deductivo parte de categorías generales para hacer afirmaciones sobre casos particulares. Va de lo general a lo particular. Es una forma de razonamiento donde se infiere una conclusión a partir de una o varias premisas. El filósofo griego Aristóteles, con el fin de reflejar el pensamiento racional, fue el primero en establecer los principios formales del razonamiento deductivo.
Por ejemplo, si se afirma que todos los seres humanos cuentan con una cabeza y dos brazos y que Pepe es un ser humano, debemos concluir que Pepe debe tener una cabeza y dos brazos. *Por ejemplo, analicemos las siguientes frases: a. ¿Cuál es verdadera y cuál es falsa?. *Otro ejemplo podría ser: Modus tollendo tollens. En lógica, el modus tollendo tollens (en latín, modo que negando niega), también llamado modus tollens y generalmente abreviado MTT o MT, es una regla de inferencia que tiene la siguiente forma: si A entonces B No B Por lo tanto, no A Por ejemplo, un razonamiento que sigue la forma del modus tollens podría ser:
Leyes de inferencia. “Si María esta despierta, entonces esta en clases” (proposición) “María no está despierta” (Proposición) “Entonces, María no está en clases” (Conclusión) Modus tollendo ponens (TP): Se conoce como la ley denegación del antecedente.
Esta ley representa una elección entre dosenunciados. . = Fui al cine. Me fui de compras.v = Es la elección (o una proposición o la otra) v “Me fui al cine o me fui de compras” (Proposición) “No fui al cine” (Proposición) “Por tanto, me fui de compras” (Conclusión) Silogismo hipotético (SH): Se conoce como razonamiento encadena. María está en la playa. Teoría de Conjuntos. Teoría de conjuntos. La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas.
Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.[1] Sin embargo, la teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de esta.
En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática. Además, la propia teoría de conjuntos es objeto de estudio per se, no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. Teoría básica de conjuntos[editar]
Graficador de Funciones Matematicas. Problema conjuntos 201. Logica y Redes. Rayuela. Pasatiempos del aula de lengua. Nivel Inicial. Juegos de lógica. Red Personal de Aprendizaje.