

Galton box animation. Galton box animation You are encouraged to solve this task according to the task description, using any language you may know.
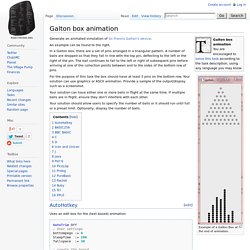
Generate an animated simulation of Sir Francis Galton's device. An example can be found to the right. Example of a Galton Box at the end of animation. In a Galton box, there are a set of pins arranged in a triangular pattern. The Normal Curve and Galton's Board. Quincunx.pdf. Pascal's triangle. Rows zero to five of Pascal's triangle In mathematics, Pascal's triangle is a triangular array of the binomial coefficients.
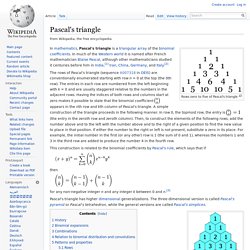
In much of the Western world it is named after French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in India,[1] Iran, China, Germany, and Italy.[2] Pascal's triangle. Pascal's triangle. Patterns in Pascal's Triangle. Pascal's Triangle conceals a huge number of various patterns, many discovered by Pascal himself and even known before his time.
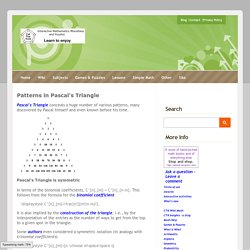
Pascal's Triangle is symmetric In terms of the binomial coefficients, C^{n}_{m} = C^{n}_{n-m}. This follows from the formula for the binomial coefficient \displaystyle C^{n}_{m}=\frac{n!} Pascal's Triangle and The Binomial Theorem. Good job, mathronaut!
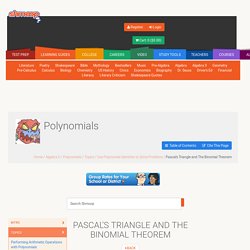
Mathrecreation: Higher Polygonal Numbers and Pascal's Triangle. The third diagonal column in Pascal's Triangle (r = 2 in the usual way of labeling and numbering) consists of the triangular numbers (1, 3, 6, 10, ...) - numbers that can be arranged in 2-dimensional triangular patterns.
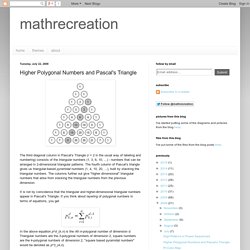
The fourth column of Pascal's triangle gives us triangular-based pyramidal numbers (1, 4, 10, 20, ...), built by stacking the triangular numbers. The columns further out give "higher dimensional" triangular numbers that arise from stacking the triangular numbers from the previous dimension. It is not by coincidence that the triangular and higher-dimensional triangular numbers appear in Pascal's Triangle. If you think about layering of polygonal numbers in terms of equations, you get In the above equation p^d_(k,n) is the nth k-polygonal number of dimension d. From the sum above, you can obtain this equation: Pascal's Triangle. Pascal's Triangle. A Group-theoretical Generalization of Pascal's Triangle. Open Archive We introduce a class of infinite triangles with rational entries generalizing Pascal's triangle.
This construction is motivated by a recent investigation concerning the growth behaviour and the asymptotics of the number of torsion-free subgroups of finite index in a finitely generated virtually free group. We show that ‘most’ of these triangles enjoy the unimodal property, and we discern which triangles have the property that the sum of the reciprocal values of the entries in the interior of a row converges to 0. 1.W. Dicks, M.J. Code golf - Pascal's Pyramid and Higher Dimensions. Pascal's Triangle is a familiar mathematical construct with many interesting properties.
Combinatorics and Reasoning: Representing, Justifying and Building Isomorphisms - كتب Google. Viewcontent. FUNDAMENTALS OF DISCRETE MATHEMATICAL STRUCTURES - K. R. CHOWDHARY - كتب Google. This thoroughly revised and updated text, now in its Second Edition, continues to provide the basic concepts of discrete mathematics and its applications at an appropriate level of rigour.
The text teaches mathematical logic, discusses how to work with discrete structures, analyzes combinatorial approach to problem-solving and develops an ability to create and understand mathematical models and algorithms essentials for writing computer programs. Every concept introduced in the text is first explained from the point of view of mathematics, followed by its relation to Computer Science. In addition, it offers excellent coverage of graph theory, mathematical reasoning, foundational material on set theory, relations and their computer representation, supported by a number of Worked-out Examples and Exercises to reinforce the students’ skill. Includes more questions in chapter-end Exercises. Galtonboard / Galtonbrett Simulation (or Bean machine or quincunx or Galton box) GENERATING IDEALS IN COMMUTATIVE ARTINIAN GROUP RINGS AND A GENERALIZE D PASCAL'S TRIANGLE.
High Order Finite Elements for Microsystems Simulation - Muhammad Razi Abdul Rahman - كتب Google. Magic Numbers and the Pascal Triangle. Magic Numbers and the Pascal Triangle "One of the main nuclear features which led to the development of the shell structure is the existence of what are usually called the magic numbers.That such numbers exist was first remarked by Elsasser in 1933.

What makes a number magic is that a configuration of a magic number of neutrons,or of protons, is unusually stable whatever the associated number of the other nucleons. When Teller and I worked on a paper on the origin of the elements, I stumbled over the magic number.We found that there were a few nuclei which have a greater isotopic as well as cosmic abundance than our theory of any other reasonable continum theory could possible explain.Then I found that those nuclei had something in common:they either had 82 neutrons, whatever the associated proton number, or 50 neutrons.Eighty-two and fiftu are magic numbers.
Maria Goppert Mayer : " The shell model" Omar Khayyam. Omar Khayyam Omar Khayyam's full name was Ghiyath al-Din Abu'l-Fath Umar ibn Ibrahim Al-Nisaburi al-Khayyami.

Khayyam studied philosophy at Naishapur. He lived in a time that did not make life easy for learned men unless they had the support of a ruler at one of the many courts. However Khayyam was an outstanding mathematician and astronomer and he did write several works including Problems of Arithmetic, a book on music, and one on algebra before he was 25 years old. In the latter, Khayyam considered the problem of finding a right triangle having the property that the hypotenuse equals the sum of one leg plus the altitude on the hypotenuse.
In 1070 he moved to Samarkand in Uzbekistan, one of the oldest cities of Central Asia. Also in his algebra book, Khayyam refers to another work of his which is now lost. In another book, Khayyam made a contribution to non-euclidean geometry, although this was not his intention. Pascal's triangle - Wikipedia, the free encyclopedia. From Wikipedia, the free encyclopedia (Redirected from Pascal triangle) The first five rows of Pascal's triangle In mathematics, Pascal's triangle is a geometric arrangement of the binomial coefficients in a triangle. It is named after Blaise Pascal in much of the western world, although other mathematicians studied it centuries before him in India, Persia, China, and Italy. Pascal's Triangle and the Binomial Coefficients.
Pascal's triangle by Jillian Williamson on Prezi. Pascal's Triangle ring of 6 numbers? Pascal's Triangle: The Story of Chance and Risk. Patterns in Pascal's Triangle - with a Twist - Cross Products of Cyclic Groups. Let us see what happens when we make a PascGalois triangle using the group Z2 x Z2. Remember that the multiplication table for this group is Now we have to choose which elements to place down the sides of our triangle. Notice that if we chose to place (0,1) down both sides, combining (0,1) with itself gives (0,0) and combining again with (0,1) gives (0,1) again so the element (0,1) cannot generate the whole group.
Patterns in Pascal's Triangle - with a Twist - Introduction. Mathematics is, at heart, a search for patterns and for a deep understanding of how and why they occur. It does not matter if the patterns are in naturally occurring phenomena -- e.g., weather or population growth -- or in geometrical structures that we mentally impose upon reality to make sense of it -- e.g., triangles, circles, ellipses, or tetrahedra.
These patterns may also be found in structures that we create for any number of reasons. We will introduce you to some structures we have been studying and some of the questions that arise from investigating the patterns we see in them. We are addressing primarily the non-specialist in mathematics, although we also include asides for mathematicians, particularly those who teach non-specialists. These asides can be found by clicking on the buttons with musical notes -- see the figure at the right, which in fact links to the first such aside. Patterns in Pascal's Triangle - with a Twist - Second Twist: Finite Groups.
The algorithm we used to generate Pascal's Triangle we can generalize still further. There is nothing special about addition -- all we need for our algorithm to work is an operation with two inputs and one output, both from the same collection of possible inputs and outputs. When we add 1 + 2 to get 3, 1 and 2 are the "inputs" and 3 is the "output". 1, 2 and 3 are all from the same set of allowable numbers. LeavittSusan_Fina_%20070311_LA.pdf. The biggest mystery you never knew about Pascal's triangle. Pascal.pdf. AsplundCCSS09.pdf.