

Conjecture de Goldbach. Catalan's conjecture. For Catalan's aliquot sequence conjecture, see aliquot sequence.
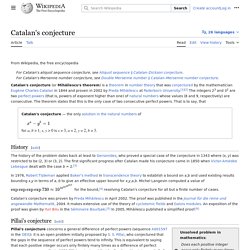
Catalan's conjecture (or Mihăilescu's theorem) is a theorem in number theory that was conjectured by the mathematician Eugène Charles Catalan in 1844 and proven in 2002 by Preda Mihăilescu. 23 and 32 are two powers of natural numbers whose values (8 and 9, respectively) are consecutive. The theorem states that this is the only case of two consecutive powers. That is to say, that the only solution in the natural numbers of. Identité remarquable. Représentation graphique de l'identité remarquable Identités remarquables du second degré[modifier | modifier le code] Dans toute la suite, a et b désignent des nombres, qui peuvent être des entiers, des rationnels et réels, ou même des complexes.
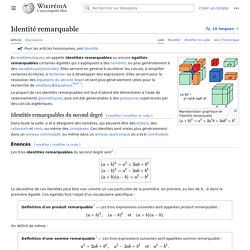
Ces identités sont vraies plus généralement dans un anneau commutatif, ou même dans un anneau quelconque où a et b commutent. Énoncés[modifier | modifier le code] Les trois identités remarquables du second degré sont[1] : Nombre premier. Nombres naturels de zéro à cent.
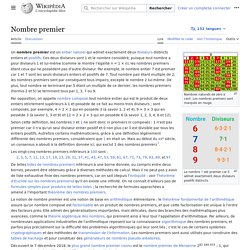
Les nombres premiers sont marqués en rouge. Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs. Ces deux diviseurs sont 1 et le nombre considéré, puisque tout nombre a pour diviseurs 1 et lui-même (comme le montre l’égalité n = 1 × n), les nombres premiers étant ceux qui n’en possèdent aucun autre. Par exemple, le nombre entier 7 est premier car 1 et 7 sont les seuls diviseurs entiers et positifs de 7. Par opposition, on appelle nombre composé tout nombre entier qui est le produit de deux entiers strictement supérieurs à 1 et possède de ce fait au moins trois diviseurs ; sont composés, par exemple, 4 = 2 × 2 qui en possède 3 (à savoir 1, 2 et 4), 9 = 3 × 3 qui en possède 3 (à savoir 1, 3 et 9) et 12 = 2 × 2 × 3 qui en possède 6 (à savoir 1, 2, 3, 4, 6 et 12).
Éléments historiques[modifier | modifier le code] Jalons symboliques[modifier | modifier le code] Algorithme d'Euclide. En mathématiques, l'algorithme d'Euclide est un algorithme qui calcule le plus grand commun diviseur (PGCD) de deux entiers, c'est-à-dire le plus grand entier qui divise les deux entiers, en laissant un reste nul.
L'algorithme ne connaît pas la factorisation de ces deux nombres. Histoire[modifier | modifier le code] Peinture censée représenter le mathématicien Euclide d'Alexandrie, par Justus of Ghent. Lemme de Gauss. Un article de Wikipédia, l'encyclopédie libre.
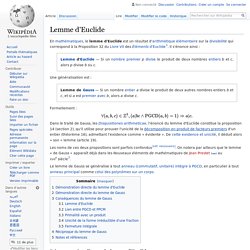
En mathématiques, le lemme d'Euclide est un résultat d'arithmétique élémentaire sur la divisibilité qui correspond à la Proposition 32 du Livre VII des Éléments d'Euclide[1]. Il s'énonce ainsi : Une généralisation est : Lemme de Gauss — Si un nombre entier a divise le produit de deux autres nombres entiers b et c, et si a est premier avec b, alors a divise c. Formellement : Équation diophantienne. Un article de Wikipédia, l'encyclopédie libre.
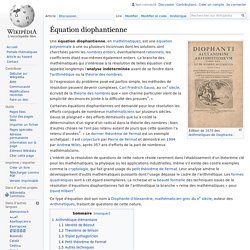
Une équation diophantienne, en mathématiques, est une équation polynomiale à une ou plusieurs inconnues dont les solutions sont cherchées parmi les nombres entiers, éventuellement rationnels, les coefficients étant eux-mêmes également entiers. La branche des mathématiques qui s'intéresse à la résolution de telles équation s'est appelée longtemps l'analyse indéterminée avant de se fondre dans l'arithmétique ou la théorie des nombres.
Si l'expression du problème posé est parfois simple, les méthodes de résolution peuvent devenir complexes. Carl Friedrich Gauss, au XIXe siècle, écrivait de la théorie des nombres que « son charme particulier vient de la simplicité des énoncés jointe à la difficulté des preuves[1]. » Certaines équations diophantiennes ont demandé pour leur résolution les efforts conjugués de nombreux mathématiciens sur plusieurs siècles. Équation diophantienne ax + by = c. Un article de Wikipédia, l'encyclopédie libre.
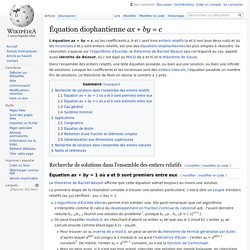
Dans l'ensemble des entiers relatifs, une telle équation possède, ou bien aucune solution, ou bien une infinité de solutions. Lorsque les coefficients et les inconnues sont des entiers naturels, l'équation possède un nombre fini de solutions. Le théorème de Paoli en donne le nombre à 1 près. Recherche de solutions dans l'ensemble des entiers relatifs[modifier | modifier le code] Équation ax + by = 1 où a et b sont premiers entre eux[modifier | modifier le code] Le théorème de Bachet-Bézout affirme que cette équation admet toujours au moins une solution.
Théorème des deux carrés de Fermat. Il s’inscrit dans la longue histoire de la représentation de nombres comme sommes de carrés qui remonte à l'Antiquité.
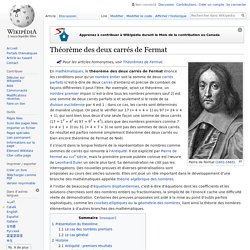
Il est explicité par Pierre de Fermat au XVIIe siècle, mais la première preuve publiée connue est l'œuvre de Leonhard Euler un siècle plus tard. Sa démonstration ne clôt pas les interrogations. Des nouvelles preuves et diverses généralisations sont proposées au cours des siècles suivants. Elles ont joué un rôle important dans le développement d’une branche des mathématiques appelée théorie algébrique des nombres. Théorème des quatre carrés de Lagrange. Un article de Wikipédia, l'encyclopédie libre.
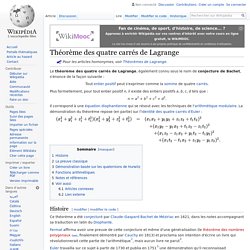
Le théorème des quatre carrés de Lagrange, également connu sous le nom de conjecture de Bachet, s'énonce de la façon suivante : Plus formellement, pour tout entier positif n, il existe des entiers positifs a, b, c, d tels que : n = a2 + b2 + c2 + d2. Il correspond à une équation diophantienne qui se résout avec les techniques de l'arithmétique modulaire. La démonstration du théorème repose (en partie) sur l'identité des quatre carrés d'Euler : Histoire[modifier | modifier le code] Ce théorème a été conjecturé par Claude-Gaspard Bachet de Méziriac en 1621, dans les notes accompagnant sa traduction en latin du Diophante.
Fermat affirma avoir une preuve de cette conjecture et même d'une généralisation (le théorème des nombres polygonaux (en), finalement démontré par Cauchy en 1813) et proclama son intention d'écrire un livre qui révolutionnerait cette partie de l'arithmétique[1], mais aucun livre ne parut[2]. Voir aussi[modifier | modifier le code] Somme de carrés - théorème de caractérisation. Nombre polygonal. Un article de Wikipédia, l'encyclopédie libre.
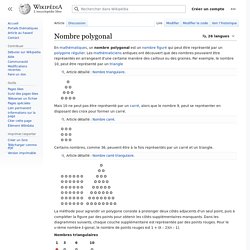
En mathématiques, un nombre polygonal est un nombre figuré qui peut être représenté par un polygone régulier. Les mathématiciens antiques ont découvert que des nombres pouvaient être représentés en arrangeant d'une certaine manière des cailloux ou des graines. Par exemple, le nombre 10, peut être représenté par un triangle Mais 10 ne peut pas être représenté par un carré, alors que le nombre 9, peut se représenter en disposant des croix pour former un carré. Certains nombres, comme 36, peuvent être à la fois représentés par un carré et un triangle. La méthode pour agrandir un polygone consiste à prolonger deux côtés adjacents d'un seul point, puis à compléter la figure par des points pour obtenir les côtés supplémentaires manquants.
Disquisitiones arithmeticae. Un article de Wikipédia, l'encyclopédie libre. Couverture de la première édition. Disquisitiones arithmeticae est un livre de théorie des nombres écrit par le mathématicien allemand Carl Friedrich Gauss. Sa première publication date de 1801. Dans ce livre, Gauss réorganise le domaine en incluant des résultats obtenus par certains de ses prédécesseurs, comme Fermat, Euler, Lagrange ou Legendre, mais ajoute surtout des contributions importantes, qu'il s'agisse de notions (comme celle de congruence), de théorèmes (comme les critères de construction à la règle et au compas d'un polygone régulier dans un cercle) ou de démonstrations (comme les premières preuves de la loi de réciprocité quadratique).
Lu et retravaillé par de nombreux mathématiciens au cours des deux derniers siècles, le livre a instauré des normes de rigueur nouvelles et a eu un impact décisif sur des sujets aussi variés que la théorie de Galois, les tests de primalité ou la théorie des idéaux[1]. Section 1. Section 2. Et. Arithmétique modulaire. Un article de Wikipédia, l'encyclopédie libre. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un ensemble de méthodes permettant la résolution de problèmes sur les nombres entiers. Ces méthodes dérivent de l’étude du reste obtenu par une division euclidienne. L'idée de base de l'arithmétique modulaire est de travailler non sur les nombres eux-mêmes, mais sur les restes de leur division par quelque chose. Quand on fait par exemple une preuve par neuf à l'école primaire, on effectue un peu d'arithmétique modulaire sans le savoir : le diviseur est alors le nombre 9.
Si ses origines remontent à l’Antiquité, les historiens associent généralement sa naissance à l’année 1801, date de la publication du livre Disquisitiones arithmeticae[1] de Carl Friedrich Gauss. L’article « Congruence sur les entiers » propose une introduction plus mathématique ; « Anneau ℤ/nℤ » traite le même sujet de manière moins didactique et plus exhaustive. et. Entier de Gauss. Pour les articles homonymes, voir Entier. En mathématiques, et plus précisément, en théorie algébrique des nombres, un entier de Gauss est un élément de l'anneau des entiers quadratiques de l'extension quadratique des rationnels de Gauss. Il s'agit donc d'un nombre complexe dont la partie réelle et la partie imaginaire sont des entiers relatifs.
Loi de réciprocité quadratique. Théorème de la progression arithmétique. Un article de Wikipédia, l'encyclopédie libre. Johann Peter Gustav Lejeune Dirichlet, auteur du théorème. En mathématiques, et plus particulièrement en théorie des nombres, le théorème de la progression arithmétique, dû au mathématicien allemand Gustav Lejeune Dirichlet, est une généralisation du théorème d'Euclide sur les nombres premiers qui s'énonce de la façon suivante : « Si m et n sont deux entiers premiers entre eux et si n est strictement positif, il existe une infinité de nombres premiers de la forme m + an avec a entier. » ce qui est équivalent à l'énoncé suivant : « Si m et n sont deux entiers premiers entre eux et si n est strictement positif, il existe une infinité de nombres premiers dans la classe de m modulo n. »
Théorème de Wilson. Théorème de Vinogradov. From Wolfram MathWorld. The prime number theorem gives an asymptotic form for the prime counting function , which counts the number of primes less than some integer . Legendre (1808) suggested that for large with (where is sometimes called Legendre's constant), a formula which is correct in the leading term only, (Nagell 1951, p. 54; Wagon 1991, pp. 28-29; Havil 2003, p. 177). In 1792, when only 15 years old, Gauss proposed that. Conjecture abc. Nombre p-adique. Nombres p-adiques.