

Théorie de la complexité (informatique théorique) Un article de Wikipédia, l'encyclopédie libre.
La théorie de la complexité est un domaine des mathématiques, et plus précisément de l'informatique théorique, qui étudie formellement la quantité de ressources (en temps et en espace) nécessaire pour la résolution de problèmes au moyen de l'exécution d'un algorithme. Il s'agit donc d'étudier la difficulté intrinsèque de problèmes posés mathématiquement. Un algorithme répond à un problème. Il est composé d'un ensemble d'étapes simples nécessaires à la résolution, dont le nombre varie en fonction du nombre d'éléments à traiter. D'autre part, plusieurs algorithmes peuvent répondre à un même problème. Machine de Turing. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir Turing. Problème de décision. Thèse de Church. Un article de Wikipédia, l'encyclopédie libre.
La thèse de Church – du nom du mathématicien Alonzo Church – est une thèse concernant la définition de la notion de calculabilité. Dans une forme dite « physique »[1], elle affirme que la notion physique de la calculabilité, définie comme étant tout traitement systématique réalisable par un processus physique ou mécanique, peut être exprimée par un ensemble de règles de calcul, défini de plusieurs façons dont on a pu démontrer mathématiquement qu'elles sont équivalentes. Dans sa forme dite « psychologique »[1] elle affirme que la notion intuitive de calculabilité, qui est liée à ce qu'un être humain considère comme effectivement calculable ou non, peut également être exprimée par ces mêmes ensembles de règles de calcul formelles. Stephen Kleene a appelé le premier « thèse de Church » (en 1943 et 1952) ce que ce dernier présentait comme une définition de la calculabilité effective.
Problème NP-complet. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir NP. Il est possible de vérifier une solution efficacement (en temps polynomial) ; la classe des problèmes vérifiant cette propriété est notée NP.Tous les problèmes de la classe NP se ramènent à celui-ci via une réduction polynomiale ; cela signifie que le problème est au moins aussi difficile que tous les autres problèmes de la classe NP. Un problème NP-difficile est un problème qui remplit la seconde condition, et donc peut être dans une classe de problème plus large et donc plus difficile que la classe NP. Bien qu'on puisse vérifier rapidement toute solution proposée d'un problème NP-complet, on ne sait pas en trouver efficacement. C'est le cas, par exemple, du problème du voyageur de commerce ou de celui du problème du sac à dos.
Définition formelle[modifier | modifier le code] Les classes et sont incluses dans , et disjointes si. Liste de problèmes NP-complets. Ceci est une liste des problèmes NP-complets les plus connus en théorie de la complexité des algorithmes, exprimés sous la forme d'un problème de décision.
Puisqu'on connaît plus de 3000 problèmes NP-complets, cette liste n'est pas exhaustive. La plupart des problèmes énumérés proviennent du livre fondamental de Garey et Johnson : Computers and Intractability: A Guide to the Theory of NP-Completeness[1]. Ils sont présentés ici suivant les mêmes ordre et organisation. Géométrie algorithmique[modifier | modifier le code] Théorie des graphes[modifier | modifier le code] Couverture et découpage en partitions[modifier | modifier le code] Sous-graphes et super-graphes[modifier | modifier le code] Complet (complexité) Problème P = NP. Un article de Wikipédia, l'encyclopédie libre.
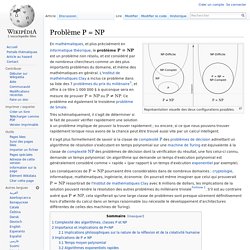
Représentation visuelle des deux configurations possibles. En mathématiques, et plus précisément en informatique théorique, le problème P = NP est un problème non résolu, et est considéré par de nombreux chercheurs comme un des plus importants problèmes du domaine, et même des mathématiques en général. L'Institut de mathématiques Clay a inclus ce problème dans sa liste des 7 problèmes du prix du millénaire[1], et offre à ce titre 1 000 000 $ à quiconque sera en mesure de prouver P = NP ou P ≠ NP. Ce problème est également le troisième problème de Smale. Très schématiquement, il s'agit de déterminer si le fait de pouvoir vérifier rapidement une solution à un problème implique de pouvoir la trouver rapidement ; ou encore, si ce que nous pouvons trouver rapidement lorsque nous avons de la chance peut être trouvé aussi vite par un calcul intelligent.
Complexité des algorithmes, classes P et NP[modifier | modifier le code] [Woeginger 1]. avec. Théorème de Fagin. Un article de Wikipédia, l'encyclopédie libre.
Ce résultat est remarquable, puisqu'il caractérise la classe NP sans avoir recours à un formalisme comme la machine de Turing. La preuve de ce résultat fut établie en 1973 par Ronald Fagin dans sa thèse de doctorat. Elle a été depuis reformulée et améliorée, notamment grâce au théorème de Lynch et à des résultats de Grandjean.
Problème SAT. Un article de Wikipédia, l'encyclopédie libre.
En informatique théorique, problème SAT est un problème de décision défini par des formules logiques. Il s'agit, étant donné une formule de logique propositionnelle, de décider si cette formule possède une solution, c'est-à-dire s'il existe une assignation des variables rendant la formule vraie. Le terme SAT est repris de l'anglais où il est extrait de la locution boolean SATisfiability problem, qui signifie problème de satisfaisabilité booléenne.
Définitions[modifier | modifier le code] Clause et forme clausale[modifier | modifier le code] Théorème de Cook. Un article de Wikipédia, l'encyclopédie libre.
Le théorème de Cook ou théorème de Cook-Levin est un théorème fondamental de la théorie de la complexité des algorithmes. Il a été démontré en 1971 par Stephen Cook[1] et, sensiblement au même moment, par Leonid Levin. Il affirme que le problème SAT est NP-complet, permettant ainsi de classer beaucoup d'autres problèmes, par réduction polynomiale.