

Groupe (mathématiques) Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir Groupe. En mathématiques, un groupe est une des structures algébriques fondamentales de l'algèbre générale. Frucht's theorem. Proof idea[edit] The main idea of the proof is to observe that the Cayley graph of G, with the addition of colors and orientations on its edges to distinguish the generators of G from each other, has the desired automorphism group.
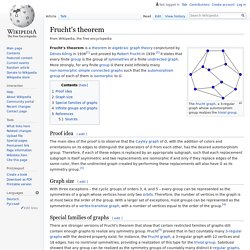
Therefore, if each of these edges is replaced by an appropriate subgraph, such that each replacement subgraph is itself asymmetric and two replacements are isomorphic if and only if they replace edges of the same color, then the undirected graph created by performing these replacements will also have G as its symmetry group.[3] History of group theory. Early 19th century[edit] The earliest study of groups as such probably goes back to the work of Lagrange in the late 18th century.
However, this work was somewhat isolated, and 1846 publications of Augustin Louis Cauchy and Galois are more commonly referred to as the beginning of group theory. Sous-groupe normal. Groupe quotient. Un article de Wikipédia, l'encyclopédie libre.
Partition d'un groupe en classes modulo un sous-groupe[modifier | modifier le code] Les classes à droite sont définies de manière analogue : Hg = { hg | h ∈ H }. Elles sont aussi les classes d'équivalence pour une relation d'équivalence convenable et leur nombre est aussi égal à [G:H]. Indice d'un sous-groupe. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir indice. Définition[modifier | modifier le code] Soient (G,•) un groupe et H un sous-groupe de G. La relation x–1y∈H est une relation d'équivalence (en x et y) dans G et les classes d'équivalence correspondantes sont les parties de G de la forme xH, où x parcourt G. On appelle ces parties de G' les classes à gauche (d'éléments de G) suivant H, ou encore modulo H. De même, la relation yx–1∈H est une relation d'équivalence dans G et les classes d'équivalence correspondantes sont les parties de G de la forme Hx, où x parcourt G. (Il est clair que les classes à gauche et les classes à droite d'éléments de G modulo H coïncident si G est commutatif. Produit direct (groupes) Un article de Wikipédia, l'encyclopédie libre.
En mathématiques, et plus particulièrement en théorie des groupes, le produit direct d'une famille de groupes est une structure de groupe qui se définit naturellement sur le produit cartésien des ensembles sous-jacents à ces groupes. Soient et. Produit semi-direct. Treillis des sous-groupes. Un article de Wikipédia, l'encyclopédie libre.
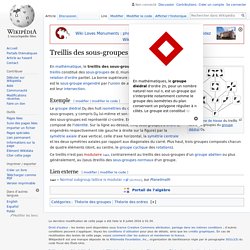
Exemple[modifier | modifier le code] Ce treillis n'est pas modulaire (en), contrairement au treillis des sous-groupes d'un groupe abélien ou plus généralement, au (sous-)treillis des sous-groupes normaux d'un groupe. Lien externe[modifier | modifier le code] (en) « Normal subgroup lattice is modular » [archive], sur Planetmath Portail de l’algèbre. Groupe abélien. Un article de Wikipédia, l'encyclopédie libre.
On sait classifier de façon simple et explicite les groupes abéliens de type fini à isomorphisme près, et en particulier décrire les groupes abéliens finis. Définition[modifier | modifier le code] est abélien, ou commutatif, lorsque la loi de composition interne du groupe est commutative, c'est-à-dire lorsque : Groupe abélien libre. Un article de Wikipédia, l'encyclopédie libre.
Exemple et contre-exemple[modifier | modifier le code] Le groupe G = ℤ⊕ℤ ≃ ℤ×ℤ, somme directe de deux copies du groupe cyclique infini ℤ, est abélien libre de rang 2, de base B = {e1,e2} avec e1 = (1, 0) et e2 = (0, 1), puisque tout élément (n, m) de G s'écrit de manière unique sous la forme (n, m) = ne1 + me2.Aucun groupe abélien fini non réduit au neutre n'est abélien libre, d'après la propriété 5 ci-dessous (pour d'autres contre-exemples cf. propriétés 5 et 6). Terminologie[modifier | modifier le code] Contrairement aux espaces vectoriels, les groupes abéliens n'ont pas tous une base, c'est pourquoi l'on réserve à ceux qui en ont une le qualificatif supplémentaire de « libres ». Ce qualificatif de « libre » peut prêter à confusion. Groupe cyclique. Un article de Wikipédia, l'encyclopédie libre.
Les groupes cycliques sont importants en algèbre. On les retrouve, par exemple, en théorie des anneaux et en théorie de Galois. Partie génératrice d'un groupe. Un article de Wikipédia, l'encyclopédie libre.
Un groupe est dit de type fini lorsqu'il admet une partie génératrice finie[1]. Un groupe engendré par un seul élément est isomorphe soit au groupe additif des entiers relatifs (ℤ, +), soit à un groupe additif de classes modulo n (ℤ/nℤ, +) ; on dit que c'est un groupe monogène. Les sous-groupes des groupes commutatifs de type fini sont également de type fini, mais cela n'est pas vrai sans hypothèse de commutativité. Théorème de Lagrange sur les groupes. Un article de Wikipédia, l'encyclopédie libre. Si G est le groupe des entiers modulo 8, alors {0, 4} forme un sous-groupe H. Sur l'exemple, {0, 4} contient 2 éléments et 2 divise 8. Énoncé[modifier | modifier le code] Démonstration[modifier | modifier le code] Remarquons que cette formule reste vraie quand les trois cardinaux qu'elle relie sont infinis, et qu'elle est un cas particulier de la formule des indices. Applications[modifier | modifier le code]
Patit théorème de Fermat. Théorème d'Euler (arithmétique) Un article de Wikipédia, l'encyclopédie libre. En mathématiques, le théorème d'Euler en arithmétique modulaire, publié en 1761 par le mathématicien suisse Leonhard Euler[1], s'énonce ainsi : Pour tout entier n > 0 et tout entier a premier avec n (autrement dit : inversible mod n), où φ est la fonction indicatrice d'Euler et mod désigne la congruence sur les entiers. Ce théorème est une généralisation du petit théorème de Fermat, qui ne traite que le cas où n est un nombre premier. Il permet la réduction modulo n de puissances.
Par exemple, si l'on veut trouver le chiffre des unités de 7222, c'est-à-dire trouver à quel nombre entre 0 et 9 est congru 7222 modulo 10, il suffit de voir que 7 et 10 sont premiers entre eux, et que φ(10) = 4. On en déduit que Le chiffre recherché est donc 9. Ordre multiplicatif. Théorème de Cauchy (groupes) Un article de Wikipédia, l'encyclopédie libre. En mathématiques, le théorème de Cauchy, nommé en l'honneur du mathématicien Augustin Louis Cauchy, est le suivant : Théorèmes de Sylow Portail des mathématiques. Théorème de Kronecker. Un article de Wikipédia, l'encyclopédie libre. Énoncé du théorème[modifier | modifier le code] Soit G un groupe abélien fini. Les éléments de cette suite sont appelés facteurs invariants de G. Théorème de structure des groupes abéliens de type fini.
Présentation d'un groupe. Théorème de Cayley. Théorèmes de Sylow. Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir Sylow. Ces théorèmes portent le nom du mathématicien norvégien Ludwig Sylow, qui les démontra en 1872[1]. Par la suite, ils ont été partiellement généralisés au cas des groupes infinis[2]. Analyse harmonique sur un groupe abélien fini. L'analyse harmonique permet de définir la notion de transformée de Fourier ou le produit de convolution. Morphisme de groupes. Théorèmes d'isomorphisme. Action de groupe (mathématiques) Action par conjugaison. Groupe symétrique. Groupe alterné. Suite exacte. Extension de groupes. Groupe résoluble. Groupe nilpotent.