

Ensemble. Mais la notion d'ensemble est aussi une notion de base qui intervient dans à peu près tous les domaines des mathématiques.
Origines[modifier | modifier le code] La formulation en reviendrait au mathématicien Georg Cantor, qui énonçait : « Par ensemble, nous entendons toute collection M d'objets m de notre intuition ou de notre pensée, définis et distincts, ces objets étant appelés les éléments de M »[trad 1],[1]. Ceci était particulièrement novateur, s'agissant d'ensembles éventuellement infinis (ce sont ces derniers qui intéressaient Cantor). Structure (mathématiques) Un article de Wikipédia, l'encyclopédie libre.
Calcul des prédicats. Un article de Wikipédia, l'encyclopédie libre.
Le calcul des prédicats du premier ordre, ou calcul des relations, ou logique du premier ordre, ou tout simplement calcul des prédicats est une formalisation du langage des mathématiques proposée par les logiciens de la fin du XIXe siècle et du début du XXe siècle. Le trait caractéristique de la logique du premier ordre est l'introduction : Ceci permet de formuler des énoncés tels que « Tout x est P » et « Il existe un x tel que pour tout y, x entretient la relation R avec y » en symboles : et. Calcul des propositions. Un article de Wikipédia, l'encyclopédie libre.
Le calcul des propositions ou calcul propositionnel est une théorie logique qui définit les lois formelles du raisonnement. C'est la version moderne de la logique stoïcienne. C'est aussi la première étape dans la construction des outils de la logique mathématique. Introduction générale[modifier | modifier le code] Assez complexe à définir en général, la notion de proposition a fait l'objet de nombreux débats au cours de l'histoire de la logique ; l'idée consensuelle est qu'une proposition est une construction syntaxique pour laquelle il est sensé de parler de vérité. Relation d'équivalence. La notion ensembliste de relation d'équivalence est omniprésente en mathématiques.
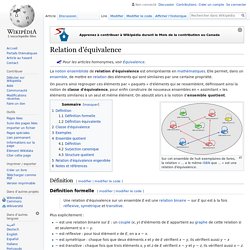
Elle permet, dans un ensemble, de mettre en relation des éléments qui sont similaires par une certaine propriété. On pourra ainsi regrouper ces éléments par « paquets » d'éléments qui se ressemblent, définissant ainsi la notion de classe d'équivalence, pour enfin construire de nouveaux ensembles en « assimilant » les éléments similaires à un seul et même élément. Relation d'ordre.
Pour les articles homonymes, voir Ordre.
Définitions et exemples[modifier | modifier le code] Relation d'ordre[modifier | modifier le code] Une relation d'ordre est une relation binaire réflexive, antisymétrique et transitive : soit E un ensemble ; une relation interne ≤ sur E est une relation d'ordre si pour tous x, y et z éléments de E : x ≤ x (réflexivité)(x ≤ y et y ≤ x) ⇒ x = y (antisymétrie)(x ≤ y et y ≤ z) ⇒ x ≤ z (transitivité) La forme même de ces axiomes permet d'affirmer que ces derniers sont également vérifiés par la relation binaire réciproque ≥, définie par y ≥ x si et seulement si x ≤ y. Majorant, borne supérieure, maximum, élément maximal. Treillis (ensemble ordonné) Un article de Wikipédia, l'encyclopédie libre.
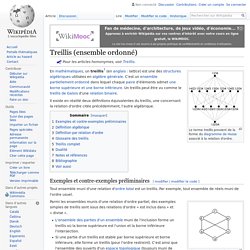
Pour les articles homonymes, voir Treillis. Le terme treillis provient de la forme du diagramme de Hasse associé à la relation d'ordre. Morphisme. Définitions[modifier | modifier le code] Cas général (théorie des modèles)[modifier | modifier le code] Soient et deux.
Filtre (mathématiques) Pour les articles homonymes, voir Filtre.
La théorie des filtres a été inventée, en 1937, par Henri Cartan[1],[2] et utilisée par Bourbaki[3]. Les filtres ont permis en particulier une démonstration élégante du théorème de Tychonov. Le cas particulier important des ultrafiltres joue un rôle fondamental dans la construction de prolongements d'objets classiques tels que les réels (donnant naissance aux hyperréels), ou les espaces localement compacts (permettant une construction du compactifié de Stone-Čech). En mathématiques, la notion de limite est au cœur de nombreux phénomènes et donne lieu à une théorie appelée topologie : (1) Si E et F sont des espaces topologiques, f est une fonction de E dans F et a est un point de E, on dit que « tend vers une limite (2) Si A est une partie non vide de la droite réelle achevée et est un point adhérent à A, on appelle limite à gauche de f au point a, relativement à A, une quantité tel que ; lorsque F est séparé, une telle quantité l est unique et notée.
Trace (théorie des ensembles) Axiome du choix. Pour tout ensemble d'ensembles non vides (les jarres), il existe une fonction qui associe à chacun de ces ensembles (ces jarres) un élément contenu dans cet ensemble (cette jarre).
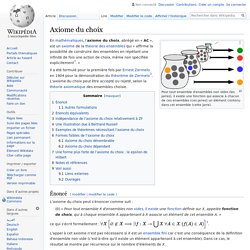
En mathématiques, l'axiome du choix, abrégé en « AC », est un axiome de la théorie des ensembles qui « affirme la possibilité de construire des ensembles en répétant une infinité de fois une action de choix, même non spécifiée explicitement[1]. » Il a été formulé pour la première fois par Ernest Zermelo en 1904 pour la démonstration du théorème de Zermelo[2]. L'axiome du choix peut être accepté ou rejeté, selon la théorie axiomatique des ensembles choisie. Énoncé[modifier | modifier le code] L'axiome du choix peut s'énoncer comme suit : Théorème de Zermelo. Un article de Wikipédia, l'encyclopédie libre. En mathématiques, le théorème de Zermelo, appelé aussi théorème du bon ordre, est un résultat de théorie des ensembles, démontré en 1904 par Ernst Zermelo, qui affirme :
Lemme de Zorn. Le lemme de Zorn permet d'utiliser l'axiome du choix sans recourir à la théorie des ordinaux (ou à celle des bons ordres via le théorème de Zermelo). En effet, sous les hypothèses du lemme de Zorn, on peut obtenir un élément maximal par une définition par récurrence transfinie, la fonction itérée étant obtenue par axiome du choix. Cependant, les constructions par récurrence transfinie sont parfois plus intuitives (quoique plus longues) et plus informatives. Il doit son nom au mathématicien Max Zorn qui, dans un article de 1935[1], en donnait le premier un grand nombre d'applications, en redémontrant des résultats connus d'algèbre. Cependant Kazimierz Kuratowski en avait déjà publié une version en 1922, et plusieurs mathématiciens, à commencer par Felix Hausdorff en 1907, avaient introduit des principes de maximalité proches du lemme de Zorn.
Ensemble inductif[modifier | modifier le code] Axiome de fondation. Théorie des ensembles. Godel.