

Théorème de la base incomplète. Un article de Wikipédia, l'encyclopédie libre.
En algèbre linéaire, le théorème de la base incomplète affirme que, dans un espace vectoriel E, En particulier, ce théorème affirme que tout espace vectoriel E admet une base. En effet, la famille vide est libre et peut être complétée en une base de E. Ce résultat d'existence, joint au théorème selon lequel toutes les bases de E ont même cardinal, conduit à la définition de la dimension d'un espace vectoriel.
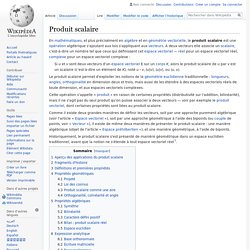
Vecteur. Deux vecteurs et.
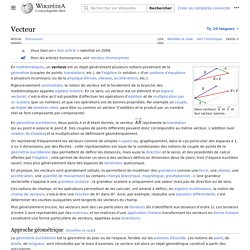
Espace vectoriel. Pour une introduction au concept de vecteur, voir l'article « Vecteur ».
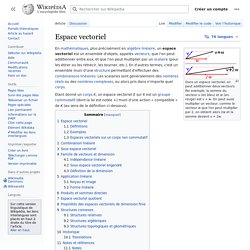
Espace vectoriel[modifier | modifier le code] Définitions[modifier | modifier le code] Soit K un corps commutatif[1],[2], comme le corps commutatif ℚ des rationnels, celui, ℝ, des réels[3] ou celui, ℂ, des complexes (on parlera dans ces cas d'espace vectoriel rationnel, réel ou complexe). Un espace vectoriel sur K, ou K-espace vectoriel, est un ensemble E, dont les éléments sont appelés vecteurs (ou — plus rarement — points[4],[5]) muni de deux lois : telles que les propriétés suivantes soient vérifiées. C'est-à-dire que pour tous vecteurs u, v et w de E : 2. C'est-à-dire que pour tous vecteurs u, v de E et tous scalaires λ, μ : Ces axiomes impliquent que E est non vide et pour tout vecteur u de E et tout scalaire λ[6] : Les vecteurs (éléments de E) ont été ici écrits avec des lettres latines italiques, mais certains auteurs les notent par des lettres en gras, ou les surmontent d'une flèche.
Matrice (mathématiques) En mathématiques, les matrices sont des tableaux des éléments (nombres, caractères) qui servent à interpréter en termes calculatoires, et donc opérationnels, les résultats théoriques de l'algèbre linéaire et même de l'algèbre bilinéaire.
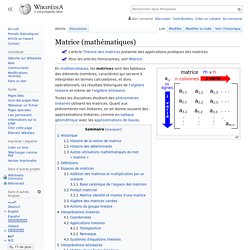
Toutes les disciplines étudiant des phénomènes linéaires utilisent les matrices. Quant aux phénomènes non linéaires, on en donne souvent des approximations linéaires, comme en optique géométrique avec les approximations de Gauss. « Dans des articles antérieurs, j'ai appelé matrix un tableau rectangulaire de termes à partir desquels plusieurs systèmes de déterminants peuvent être engendrés, comme issus des entrailles d'un parent commun »[6]. En 1854, Arthur Cayley publie un traité sur les transformations géométriques utilisant les matrices de façon beaucoup plus générale que tout ce qui a été fait avant lui. , des puissances akj par ajk. Deux mathématiciens notables au moins ont utilisé le mot dans un sens inhabituel. où p = min(m,n). Exemple : avec : Soit.
Élimination de Gauss-Jordan. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir Pivot. Histoire[modifier | modifier le code] Cette méthode est connue des Chinois depuis au moins le Ier siècle de notre ère. Elle est référencée dans le livre chinois Jiuzhang suanshu (Les Neuf Chapitres sur l'art mathématique), dont elle constitue le huitième chapitre, sous le titre « Fang cheng » (la disposition rectangulaire). Produit scalaire. Le produit scalaire permet d'exploiter les notions de la géométrie euclidienne traditionnelle : longueurs, angles, orthogonalité en dimension deux et trois, mais aussi de les étendre à des espaces vectoriels réels de toute dimension, et aux espaces vectoriels complexes.
Produit vectoriel. Un article de Wikipédia, l'encyclopédie libre.
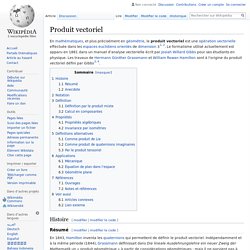
Histoire[modifier | modifier le code] Résumé[modifier | modifier le code] En 1843, Hamilton inventa les quaternions qui permettent de définir le produit vectoriel. Indépendamment et à la même période (1844), Grassmann définissait dans Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik un « produit géométrique » à partir de considérations géométriques ; mais il ne parvient pas à définir clairement un produit vectoriel.
Puis Grassmann lit Hamilton et s'inspire de ses travaux pour publier en 1862 une deuxième version de son traité qui est nettement plus claire[5]. Déterminant (mathématiques) Un domaine spécifique de l'algèbre est consacré à l'étude du déterminant et de ses généralisations : il s'agit de l'algèbre multilinéaire.
Fig. 1. Le Japonais Kowa Seki introduit le premier des déterminants de taille 3 et 4, à la même époque que l'Allemand Leibniz. L'apparition des déterminants de taille supérieure demande ensuite plus de cent ans. Curieusement, le Japonais Kowa Seki et l'Allemand Leibniz en donnèrent les premiers exemples presque simultanément.
Théorème de Cayley-Hamilton. En algèbre linéaire, le théorème de Cayley-Hamilton affirme que tout endomorphisme d'un espace vectoriel de dimension finie sur un corps commutatif quelconque annule son propre polynôme caractéristique.
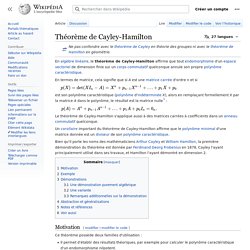
En termes de matrice, cela signifie que si A est une matrice carrée d'ordre n et si est son polynôme caractéristique (polynôme d'indéterminée X), alors en remplaçant formellement X par la matrice A dans le polynôme, le résultat est la matrice nulle[1] : Comatrice. La comatrice est aussi appelée matrice des cofacteurs.
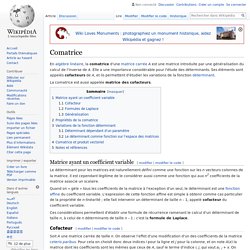
Matrice ayant un coefficient variable[modifier | modifier le code] Le déterminant pour les matrices est naturellement défini comme une fonction sur les n vecteurs colonnes de la matrice. Il est cependant légitime de le considérer aussi comme une fonction qui aux n2 coefficients de la matrice associe un scalaire. Quand on « gèle » tous les coefficients de la matrice à l'exception d'un seul, le déterminant est une fonction affine du coefficient variable. L'expression de cette fonction affine est simple à obtenir comme cas particulier de la propriété de n-linéarité ; elle fait intervenir un déterminant de taille n – 1, appelé cofacteur du coefficient variable.
Règle de Cramer. Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir Cramer. En calcul, la méthode est moins efficace que la méthode de résolution de Gauss pour des grands systèmes (à partir de quatre équations) dont les coefficients dans le premier membre sont explicitement donnés. Cependant, elle est d'importance théorique pour la raison qu'elle donne une expression explicite pour la solution du système, et elle s'applique dans des systèmes où par exemple les coefficients du premier membre dépendent de paramètres, ce qui peut rendre la méthode de Gauss inapplicable.
Elle est nommée d'après Gabriel Cramer, mathématicien suisse (1704-1752). Forme linéaire. Pour les articles homonymes, voir Forme. Les formes linéaires sur un espace vectoriel portent parfois également le nom de covecteur. Ce terme qui prend sens dans le cadre général des tenseurs et du calcul tensoriel rappelle que si les formes linéaires peuvent être représentées par un système de coordonnées comparable à celui des vecteurs, elles s'en distinguent pour ce qui est des formules de transformations. Réduction d'endomorphisme. Premier aperçu[modifier | modifier le code] Les deux premières sous-sections ci-dessous effleurent des notions essentielles approfondies plus loin.
Les deux suivantes évoquent des cas particuliers. Endomorphisme et vecteur propre[modifier | modifier le code] Deux obstacles à la diagonalisation[modifier | modifier le code] Il y a deux obstacles qui empêchent que tout endomorphisme en dimension finie soit diagonalisable.