

Les maths et la nature. Nombre d'or. Un article de Wikipédia, l'encyclopédie libre.
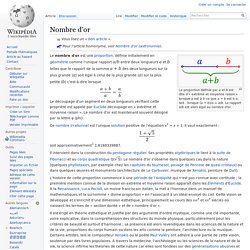
La proportion définie par a et b est dite d'« extrême et moyenne raison » lorsque a est à b ce que a + b est à a, soit : lorsque (a + b)/a = a/b. Le rapport a/b est alors égal au nombre d'or. Le nombre d'or est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b) c'est-à-dire lorsque. Les mathématiques dans la nature : géométrie plane. 1) Introduction : Les mathématiques, qu'on le veuille ou non, sont présentes partout dans la nature.
La géométrie nous entoure par ses différentes représentations sans même que nous nous en apercevions. Les escargots font-ils des maths ? - La philo en petits morceaux. Le nombre d'or. L'Homme de Vitruve de Léonard de Vinci Un nombre étonnant, mystérieux et magique pour avoir fait parler de lui depuis la plus haute antiquité dans de nombreux domaines tels que la géométrie, l’architecture, la peinture, la nature, … Il serait une expression d’harmonie et d’esthétique dans les arts bien que certains lui reproche son caractère ésotérique qui cherche absolument à lui trouver une obscure beauté et qui semble y parvenir !
On le note φ (phi) en hommage au sculpteur grec Phidias (Ve siècle avant J.C.) qui participa à la décoration du Parthénon sur l’Acropole à Athènes. Quant à son nom, il a évolué avec le temps. Le mathématicien et moine franciscain Luca Pacioli (1445 ; 1517) parle de « Divine proportion », plus tard le physicien Johannes Kepler (1571 ; 1630) le désigne comme le « joyau de la géométrie ». Le nombre d'or. (Vitruve, architecte romain 1er siècle avant notre ère). Ainsi si a et b sont les deux grandeurs alors nous aurons : a/b = (a + b) / a.
A/b = 1 + b/a pour simplifier, prenons comme variable x = a/b. alors nous obtenons : x = 1 + 1/x x - 1 - 1/x = 0 comme x non nul, nous obtenons l'équation suivante que nous noterons (E) : x2 - x - 1 = 0 qui admet comme racine positive : x = Le nombre d'or. L' histoire ...

Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d'or (temple d'Andros découvert sous la mer des Bahamas). 2800 av JC : La pyramide de Khéops a des dimensions qui mettent en évidence l'importance que son architecte attachait au nombre d'or. Vè siècle avant J-C. (447-432 av.JC) : Le sculpteur grec Phidias utilise le nombre d'or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d'Athéna Parthénos . Il utilise également la racine carrée de 5 comme rapport. IIIè siècle avant J-C. : Euclide évoque le partage d'un segment en "extrême et moyenne raison" dans le livre VI des Eléments.